Quantum Information Limits of a Classical Sensor

Return to all Research Topics

Quantum Information Limits of a Classical Sensor

The Heisenberg Uncertainty Principle (HUP) constrains the product of the uncertainty for two conjugate variables in any measurement. From this comes the well known quantum principle that you 'cannot know the position and momentum of a particle simultaneously with arbitrary precision' (cf. Feynman 37-1).

In high precision mechanical experiments (e.g. LIGO), the measurement uncertainty is dominated by the fluctuations of the electromagnetic field: the statistical fluctuations of the ground state (i.e. empty space) enter the system and produce fluctuations in any measurement. The squeezed light technique uses nonlinear optics (crystals or opto-mechanics) to introduce correlations in the field such that there more fluctuations in one of the variables and less in the other. If you want to measure the phase of the light precisely, it is not necessary to measure the amplitude precisely.

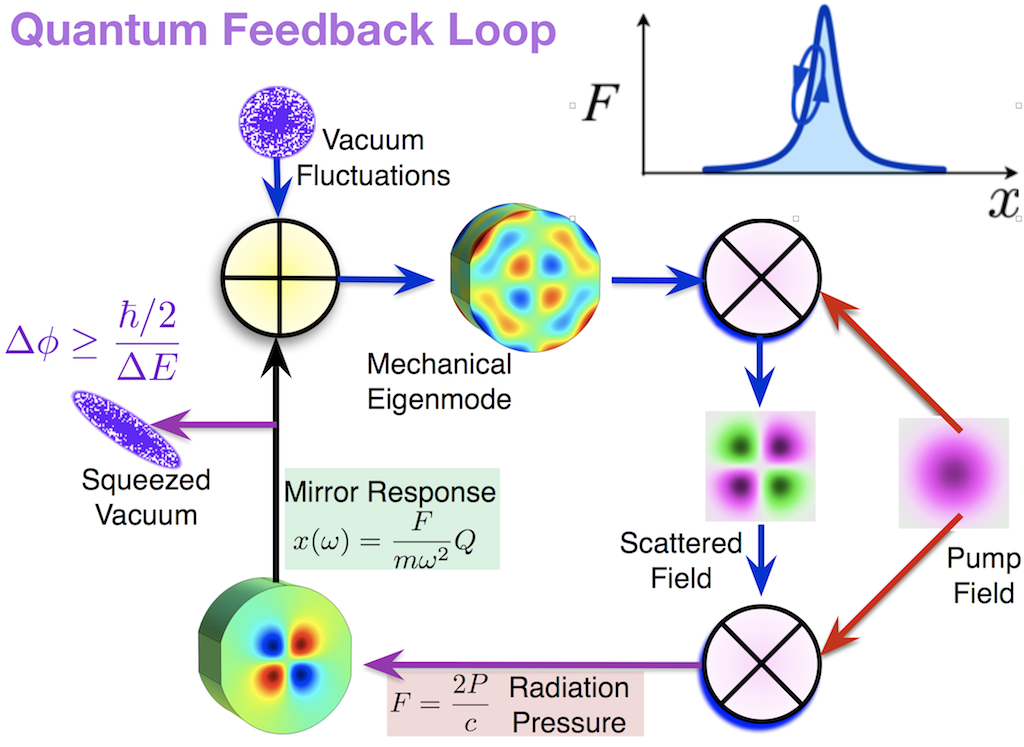At Caltech, we are working on a few projects to push the limits of measurement by exploiting this "loophole".

  1. Waveguide Squeezing: making a ultra-compact setup that can be fiber coupled, put in vacuum chambers, and sent into space.
  2. Using the opto-mechanical, radiation pressure mediated feedback in laser interferometers to make a device that squeezes itself and thereby avoids the Poisson statistics in standard quantum limits.
  3. Engineering of strong opto-mechanical quantum feedback to amplify the signals and avoid the degradation and decoherence of the entangled light.

Publications

"The Energetic Quantum Limit", by Braginsky, Thorne, Khalili https://www.aip.org/history/exhibits/einstein/essay-brownian.htm< /a>
"Evading Quantum Mechanics", by M. Tsang and Carlton Caves PRX (2012)
"Towards the Fundamental Quantum Limit of Linear Measurements of Classical Signals", by H. Miao, R. Adhikari, Y. Ma, B. Pang, Y. Chen, PRL (2017)