Phase-Sensitive Optomechanical Amplifier (PSOMA)

Gravitational-wave detectors face a fundamental quantum trade-off: reducing shot noise (by increasing laser power) increases radiation pressure noise, and vice versa. At any given frequency, the standard quantum limit (SQL) represents the best sensitivity achievable by balancing these two contributions. PSOMA — a phase-sensitive optomechanical amplifier — offers a way around this limit by amplifying the gravitational-wave signal before quantum noise contaminates the readout, making the signal large enough that downstream losses become negligible.

Contents:

• Phase-sensitive vs phase-insensitive amplification
• The PSOMA concept
• Optomechanical amplification mechanism
• Gain bandwidth and frequency dependence
• Noise budget
• The SQL and how PSOMA circumvents it
• Competing approaches to sub-SQL sensitivity
• Implementation with signal recycling and optical springs
• Connections to other EGG projects
• Our contributions
• Current status and open questions
• Key references
• Further reading

---

Phase-sensitive vs phase-insensitive amplification

An electromagnetic field has two quadratures — amplitude and phase — which together define the signal’s complete quantum state. An amplifier boosts this signal before detection. The critical question is how it treats the two quadratures.

A phase-insensitive amplifier (PIA) amplifies both quadratures equally with gain $G$. Heisenberg’s uncertainty principle then demands that it add at least half a quantum of noise per quadrature — the so-called quantum limit of amplification:

\[S_\text{added}^\text{PIA} \geq \frac{1}{2}\hbar\omega \quad \text{(per quadrature)}\]

This is the Haus-Caves theorem (Caves 1982). No matter how cleverly you build it, a PIA must add noise. For a high-gain PIA, the output signal-to-noise ratio is at best half the input SNR — a 3 dB penalty.

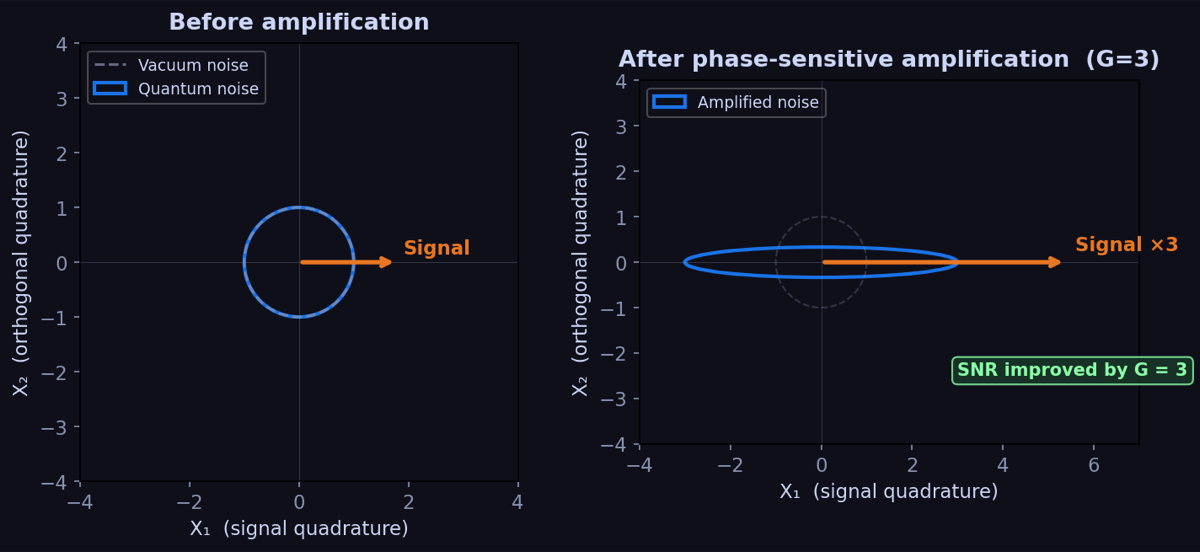
A phase-sensitive amplifier (PSA) breaks this constraint by treating the two quadratures asymmetrically. It amplifies one quadrature by gain $G$ while deamplifying the orthogonal quadrature by $1/G$. The product $G \times (1/G) = 1$ satisfies the uncertainty principle without adding any noise:

\[S_\text{added}^\text{PSA} = 0\]

Why the uncertainty principle allows noiseless amplification

The Heisenberg uncertainty principle constrains the product of uncertainties in conjugate quadratures:

\[\Delta X_1 \cdot \Delta X_2 \geq \frac{1}{2}\]

A PIA maps $X_1 \to \sqrt{G}\, X_1$ and $X_2 \to \sqrt{G}\, X_2$. The product $\Delta X_1 \cdot \Delta X_2$ grows as $G$ — far exceeding the minimum. The extra uncertainty must come from somewhere, and it comes from vacuum fluctuations entering through the amplifier’s internal mode. The Haus-Caves theorem formalizes this: the amplifier must couple to at least one additional mode, and that mode’s vacuum noise gets amplified into the output.

A PSA maps $X_1 \to \sqrt{G}\, X_1$ and $X_2 \to X_2/\sqrt{G}$. The product $\Delta X_1 \cdot \Delta X_2$ is unchanged — the minimum uncertainty is preserved without any additional noise. The price: you must know which quadrature carries the signal, and the pump phase must be locked to amplify exactly that quadrature. If the pump phase drifts by $\pi/2$, the signal quadrature is deamplified instead.

---

The PSOMA concept

The key insight from Bai, Venugopalan, Kuns, Wipf, Markowitz, Wade, Chen & Adhikari (2020) is that the amplifier can be built from optomechanical components — mirrors and light — rather than requiring exotic nonlinear crystals or atomic media. Specifically, the authors proposed using a Mach-Zehnder interferometer with suspended mirrors as the phase-sensitive amplifier, installed between the antisymmetric port of the main interferometer and the readout photodetector.

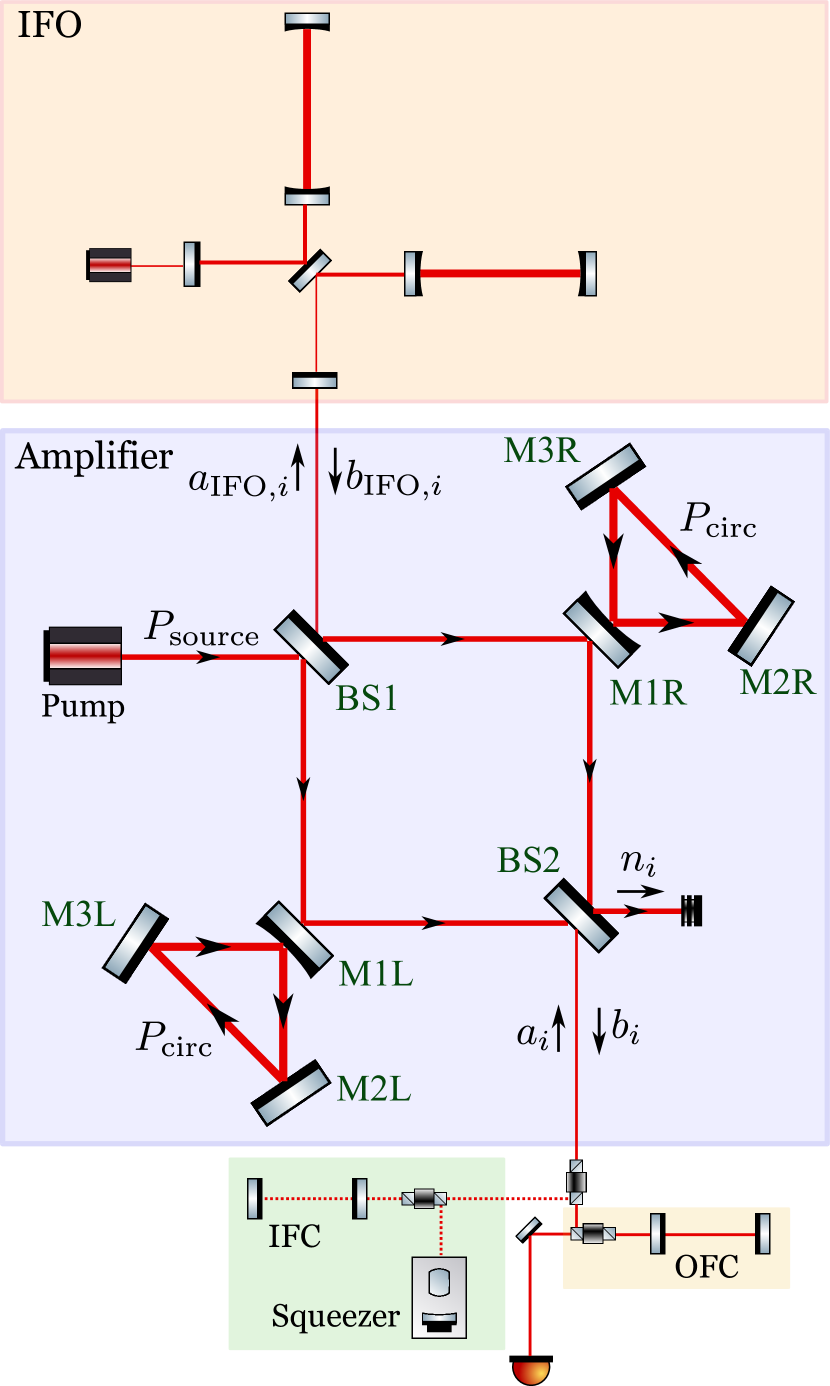
The architecture works as follows:

1. The main interferometer (IFO) produces a signal field at its antisymmetric port, encoding the gravitational-wave strain in one quadrature of the light.

2. The Mach-Zehnder amplifier receives this signal field. It contains two Fabry-Perot arm cavities with suspended mirrors, each pumped by an auxiliary laser. The optomechanical interaction — radiation pressure coupling between the pump light and the mirror motion — provides parametric gain.

3. The output field carries the amplified signal quadrature. Because the gain is phase-sensitive, the noise in the signal quadrature is not amplified — only the signal itself grows.

4. The readout chain (Faraday isolator, mode-matching telescope, photodetector) then detects the amplified field. Any losses in this chain are now harmless because the signal has already been boosted by tens of dB.

Why a Mach-Zehnder?

A single Fabry-Perot cavity with a detuned optical spring can provide optomechanical gain, but it is inherently phase-insensitive — it amplifies both quadratures. To achieve phase-sensitive amplification, two such cavities must be combined interferometrically so that the gain in one quadrature adds constructively while the gain in the orthogonal quadrature cancels.

The Mach-Zehnder configuration achieves this by splitting the signal into two paths, each containing a detuned optomechanical cavity, and then recombining them with appropriate phase shifts. The differential detuning between the two arms — one blue-detuned, one red-detuned — creates the asymmetry between quadratures that makes the amplification phase-sensitive.

This is analogous to how a balanced homodyne detector rejects common-mode noise: the Mach-Zehnder rejects the phase-insensitive component of the optomechanical gain, leaving only the phase-sensitive part.

---

Optomechanical amplification mechanism

The physics underlying PSOMA is the radiation pressure interaction between light and a mechanical oscillator. When a laser field bounces off a suspended mirror, two things happen:

1. Radiation pressure force: The light exerts a force on the mirror proportional to the circulating power. Fluctuations in the light field create fluctuating forces, which drive mirror motion.

2. Phase modulation: The mirror’s motion modulates the phase of the reflected light. This creates sidebands on the reflected field at frequencies $\omega_0 \pm \Omega$, where $\Omega$ is the mechanical oscillation frequency.

Together, these create a feedback loop: light pushes the mirror, mirror modulates the light, modulated light pushes the mirror differently. This is the optomechanical parametric interaction, and it can amplify signals.

The detuned optical spring

When a Fabry-Perot cavity is detuned from resonance (the laser frequency is offset from the cavity resonance), the radiation pressure force acquires a component proportional to the mirror displacement — an optical spring:

\[F_\text{opt} = -K_\text{opt}\, x - \gamma_\text{opt}\, \dot{x}\]

The first term is a restoring force (spring), and the second is either damping or anti-damping depending on the sign of the detuning. For blue detuning ($\omega_\text{laser} > \omega_\text{cavity}$), the optical spring provides anti-damping — energy flows from the light field into the mechanical motion, amplifying it. This is the same instability that limits the circulating power in Advanced LIGO (the parametric instability), but here it is harnessed as the amplification mechanism.

Connection to signal recycling

The PSOMA amplifier is conceptually related to signal recycling in gravitational-wave detectors. In signal recycling, a mirror is placed at the antisymmetric port to create a compound cavity that reshapes the detector’s frequency response. A detuned signal recycling cavity creates an optical resonance that amplifies signals near the detuning frequency — at the cost of narrowing the detection bandwidth.

PSOMA generalizes this idea. Instead of a single signal recycling mirror, it uses a full Mach-Zehnder interferometer with optomechanical cavities. The key advantage: because the amplification is phase-sensitive rather than phase-insensitive, it does not add the quantum noise penalty that signal recycling introduces. Signal recycling amplifies the signal but also amplifies the quantum noise in the same quadrature. PSOMA amplifies the signal while leaving the noise unchanged.

The connection to Korth, Miao, Corbitt, Cole, Chen & Adhikari (2013) — who studied quantum radiation pressure noise suppression in optical springs — is direct: that work established the theoretical framework for controlling optomechanical interactions in the quantum regime, which PSOMA builds upon.

Parametric gain

The optomechanical gain of the amplifier depends on the pump power, the cavity detuning, and the mechanical properties of the suspended mirrors. For the PSOMA configuration analyzed by Bai et al. (2020), the gain in the signal quadrature is:

\[G(\Omega) \approx \frac{4\omega_\text{opt}^2}{\Omega^2} \quad \text{for } \Omega \ll \omega_\text{opt}\]

where $\omega_\text{opt}$ is the optical spring frequency, set by the circulating power and cavity geometry. At low frequencies (below $\omega_\text{opt}$), the gain is very large — exceeding 60 dB below 30 Hz for the parameters in Bai et al. (2020). At high frequencies (above $\omega_\text{opt}$), the gain falls as $1/\Omega^2$ because the mirrors cannot respond fast enough.

This frequency-dependent gain profile is exactly what is needed: the low-frequency region (10-100 Hz) is where radiation pressure noise dominates in Advanced LIGO and where PSOMA provides the most benefit.

---

Gain bandwidth and frequency dependence

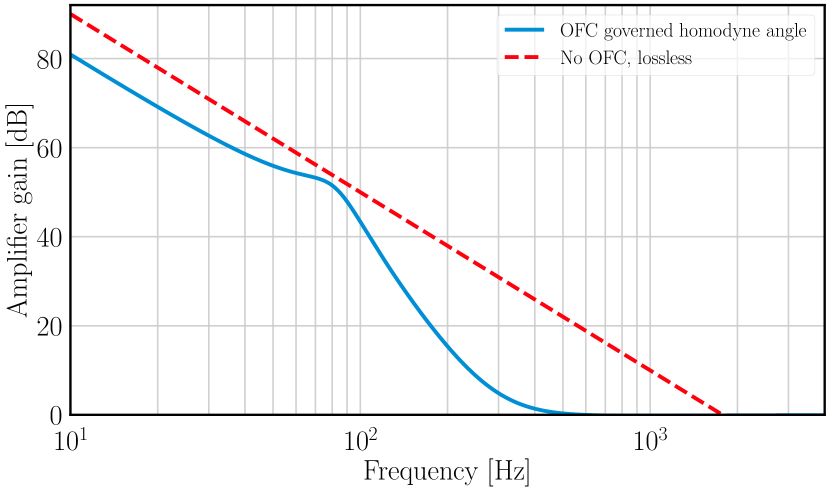
The gain spectrum reveals a critical feature of PSOMA: the amplification is strongest at low frequencies, where it is most needed.

Below ~30 Hz: Gain exceeds 60 dB (a factor of $10^3$ in amplitude). At these frequencies, radiation pressure noise dominates the quantum noise budget of Advanced LIGO and its upgrades. The enormous gain ensures that even very small signals are boosted far above the readout noise floor.

30-300 Hz: Gain rolls off but remains substantial (20-60 dB). This is the most sensitive band of current detectors, where shot noise and radiation pressure noise are comparable. PSOMA still provides significant benefit here.

Above ~500 Hz: Gain drops below 10 dB. At these frequencies, shot noise dominates and the detector is already close to optimal with frequency-dependent squeezing alone. PSOMA adds little benefit — but also adds little noise.

The role of the output Faraday circulator

The output Faraday circulator (OFC) that routes squeezed vacuum into the interferometer also determines the readout quadrature angle as a function of frequency. Bai et al. (2020) showed that the OFC’s frequency-dependent rotation of the readout angle affects the effective gain profile (solid blue vs dashed red curves in the figure above). The OFC constrains the low-frequency gain somewhat but is essential for compatibility with squeezed vacuum injection.

---

Noise budget

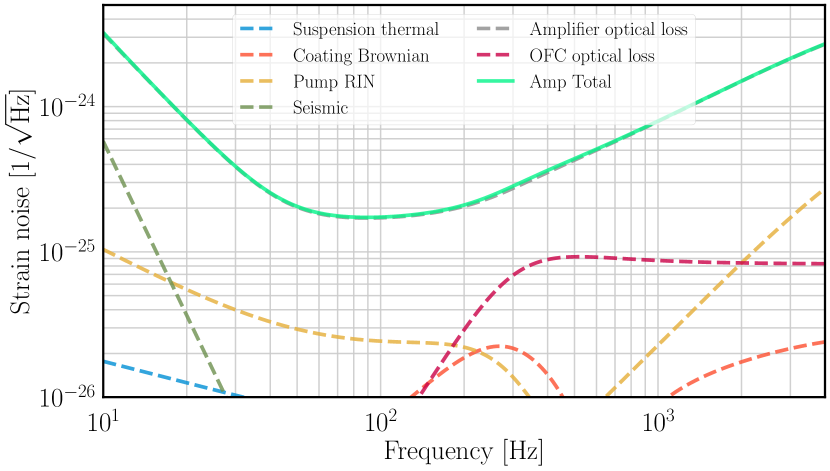
The amplifier introduces its own noise sources that must be kept below the main interferometer’s noise floor. Bai et al. (2020) performed a detailed noise budget analysis, identifying the dominant contributions:

Suspension thermal noise

The amplifier’s test masses are suspended on pendulums, just like the main interferometer optics. Thermal fluctuations in the suspension fibers create random mirror displacements that couple into the amplified output. At low frequencies (below ~20 Hz), suspension thermal noise sets the amplifier’s noise floor.

Mitigation: Use high-Q suspension materials (fused silica fibers, as in Advanced LIGO) and keep the amplifier test masses at a moderate temperature. Because the amplifier mirrors are much smaller and lighter than the main interferometer’s 40 kg test masses, the suspension design requirements are different.

Coating Brownian noise

Thermal fluctuations in the mirror coatings create apparent displacement noise. This is the same mechanism that limits Advanced LIGO’s sensitivity near 100 Hz, and it dominates the amplifier noise budget in the 100-1000 Hz band.

Mitigation: The amplifier mirrors can use the advanced coating technologies being developed for next-generation detectors — crystalline coatings (AlGaAs), ion beam-sputtered silica/tantala with doping, or amorphous silicon coatings at cryogenic temperatures. The coating thermal noise project directly addresses this challenge.

Pump relative intensity noise (RIN)

Fluctuations in the pump laser power modulate the optical spring frequency and the radiation pressure force, creating a noise pathway analogous to laser intensity noise in the main interferometer. In the PSOMA noise budget, pump RIN is significant below ~30 Hz.

Mitigation: Intensity stabilization of the pump laser to $\text{RIN} < 10^{-9}/\sqrt{\text{Hz}}$ at 10 Hz. This is comparable to the intensity stabilization already achieved for the Advanced LIGO laser.

Optical losses

Optical loss in the amplifier cavities and the output Faraday circulator degrades the phase-sensitive amplification by mixing in vacuum fluctuations. The OFC loss (magenta dashed curve) is particularly important at high frequencies, where the amplifier gain is small and cannot overcome the loss-induced noise.

Loss tolerance: why PSOMA helps even with imperfect optics

Consider readout losses of ~20% (a realistic value for the total output chain including mode-matching and photodetector inefficiency). Without PSOMA, 15 dB of injected squeezing is degraded to about 7 dB at the photodetector — the loss eats more than half the quantum advantage.

With PSOMA providing 40 dB of gain at 50 Hz, the signal arriving at the lossy readout chain is $10^4$ times larger. The 10% loss now mixes in vacuum noise that is $10^4$ times smaller relative to the signal. The effective degradation of squeezing from readout loss drops from catastrophic to negligible.

This is the core value proposition: PSOMA does not reduce noise — it makes the signal so large that downstream noise sources become irrelevant.

---

The SQL and how PSOMA circumvents it

The standard quantum limit (SQL) for a free mass arises from the trade-off between shot noise and radiation pressure noise:

\[S_h^\text{SQL}(\Omega) = \frac{8\hbar}{m\,\Omega^2\, L^2}\]

where $m$ is the mirror mass, $L$ is the arm length, and $\Omega$ is the angular frequency. Shot noise decreases with increasing laser power ($\propto 1/P$), while radiation pressure noise increases ($\propto P$). The SQL is the geometric mean — the best you can do by choosing $P$ optimally at each frequency.

Several strategies exist for beating the SQL:

1. Modify the measurement (variational readout, speed meters): Change what is measured to evade the back-action.
2. Modify the noise (squeezed light): Reduce the vacuum fluctuations entering the interferometer.
3. Amplify the signal (PSOMA): Make the signal large compared to the quantum noise floor.

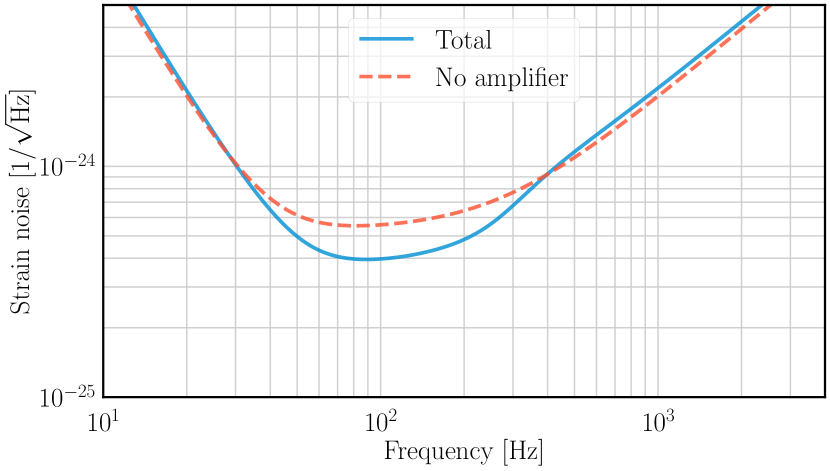
The figure shows the payoff: with PSOMA, LIGO Voyager’s strain sensitivity improves by roughly a factor of 2 in the 20-100 Hz band. Since gravitational-wave event rate scales as the cube of the detection range, this translates to approximately 8 times more detected events in the radiation-pressure-limited frequency band.

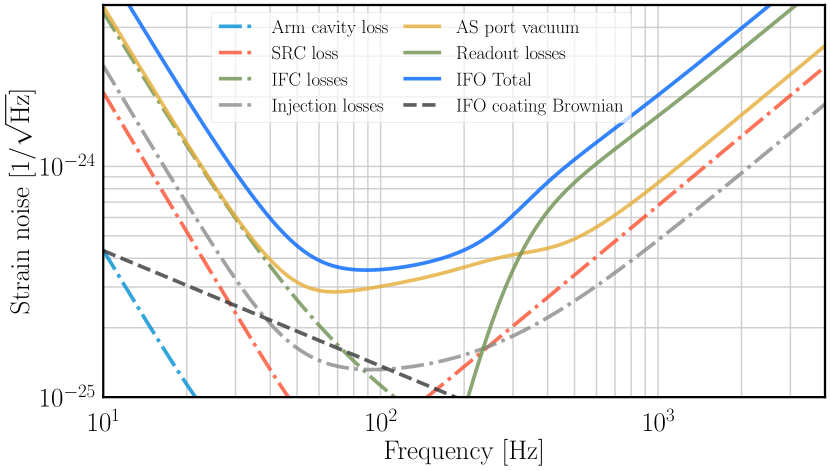
The full detector noise budget with PSOMA reveals the new limiting noise sources once quantum noise is suppressed. At low frequencies (below ~30 Hz), the arm cavity optical loss and suspension thermal noise dominate. In the 50-200 Hz band, coating Brownian noise from the main interferometer test masses sets the floor. This noise budget shows that PSOMA successfully pushes quantum noise below other fundamental limits, shifting the optimization challenge to thermal noise reduction — a problem addressed by the group’s coating thermal noise and LIGO Voyager programs.

---

Competing approaches to sub-SQL sensitivity

Several techniques have been proposed or demonstrated for surpassing the standard quantum limit. Each has different trade-offs, and PSOMA’s distinctive advantage is its tolerance of readout losses.

Frequency-dependent squeezing

Status: Deployed in LIGO A+ (Ganapathy et al. 2023).

Squeezed vacuum is injected into the interferometer’s antisymmetric port, reducing shot noise at high frequencies and radiation pressure noise at low frequencies. A 300-meter filter cavity rotates the squeeze angle as a function of frequency to achieve broadband noise reduction.

Limitation: Squeezed light is fragile. Every percent of optical loss in the readout chain degrades the squeezing. With 10% total loss, the maximum useful squeezing is ~10 dB regardless of how much is injected. Achieving 15 dB of effective squeezing (the third-generation target) requires losses below 3% — extremely challenging with current technology.

Relation to PSOMA: Complementary. Squeezing reduces the noise floor; PSOMA amplifies the signal above whatever noise floor remains. PSOMA also protects squeezed states from readout losses, making the two techniques synergistic rather than redundant.

Variational readout

Status: Proposed; not yet demonstrated in GW detectors.

By varying the homodyne detection angle as a function of frequency, one can always measure the quadrature with the best signal-to-noise ratio. Mathematically equivalent to frequency-dependent squeezing in some configurations.

Limitation: Requires the same low-loss readout chain as squeezing. Any loss in the output optics introduces vacuum noise that cannot be undone by changing the readout angle.

Speed meters

Status: R&D stage; small-scale prototypes.

Interferometer topologies (Sagnac, zero-area Sagnac, polarization-based) that measure test mass velocity rather than displacement. Velocity measurement naturally evades radiation pressure back-action because the back-action force acts on position, not velocity.

Limitation: Requires fundamentally different detector topology. Cannot be retrofitted to existing LIGO infrastructure. Sensitivity at high frequencies may be worse than position-measurement topologies.

PSOMA

Status: Theoretical proposal (Bai et al. 2020); no experimental demonstration yet.

Distinctive advantages:

• Loss tolerance: The signal is amplified before encountering lossy readout elements, making downstream losses irrelevant.
• Compatibility: Can be added to existing or planned detector designs without changing the main interferometer topology.
• Synergy with squeezing: Works alongside frequency-dependent squeezing, providing the greatest benefit precisely where squeezing is most vulnerable to loss.

Challenges:

• Requires additional suspended optics (the Mach-Zehnder amplifier cavities) with their own thermal noise contributions.
• Pump laser noise can couple into the amplified output.
• No experimental demonstration yet — the concept remains theoretical.

---

Implementation with signal recycling and optical springs

The PSOMA concept connects to several ideas in interferometer design that use optomechanical effects for signal enhancement.

Optical springs in GW detectors

When a Fabry-Perot cavity is operated off resonance, the circulating power depends on the mirror position, creating a position-dependent radiation pressure force — the optical spring. In Advanced LIGO’s signal recycling configuration, the optical spring modifies the test mass dynamics and creates a resonant enhancement of the gravitational-wave signal near the optical spring frequency.

Korth, Miao, Corbitt, Cole, Chen & Adhikari (2013) studied how quantum radiation pressure noise in optical springs can be suppressed through sensing and feedback control. That work showed that the effective mechanical quality factor of a mirror can be increased by stiffening it with an optical spring, and the associated radiation pressure noise can be evaded. This is a key building block for PSOMA: the amplifier cavities must operate in a regime where the optical spring provides gain without introducing excessive noise.

Detuned signal recycling as a precursor

Signal recycling cavities in gravitational-wave detectors have been operated in both resonant (broadband) and detuned (narrowband) configurations. Detuned signal recycling creates an optical resonance that amplifies signals near the detuning frequency, but this amplification is phase-insensitive — it amplifies both quadratures, including the noise.

PSOMA can be understood as a generalization of detuned signal recycling where the amplification is made phase-sensitive through the Mach-Zehnder topology. The interferometric combination of two detuned cavities cancels the phase-insensitive gain component, leaving only the desired phase-sensitive amplification.

Design parameters from Bai et al. (2020)

Reference parameters for a Voyager-compatible PSOMA

Bai et al. (2020) analyzed PSOMA for a LIGO Voyager-class detector with the following baseline parameters:

Parameter	Value
IFO arm length	4 km
IFO arm power	3 MW
IFO test mass	200 kg
Amplifier mirror mass	~1 kg
Amplifier cavity length	~1 m
Amplifier pump power	~100 W circulating
Optical spring frequency	~100 Hz
Peak amplifier gain	>60 dB at 10 Hz
Squeezed vacuum injection	15 dB, frequency-dependent
Readout loss (without PSOMA)	10%
Effective readout loss (with PSOMA)	Negligible at low frequencies

The amplifier mirrors are orders of magnitude lighter than the main interferometer test masses, which makes the optical spring frequency higher and allows the amplifier to respond at gravitational-wave frequencies. The trade-off is that lighter mirrors have more radiation pressure noise — but because the amplifier operates in a phase-sensitive mode, this noise is directed into the deamplified quadrature.

---

Connections to other EGG projects

PSOMA sits at the intersection of several research threads in the group:

---

Our contributions

• PSOMA proposal for gravitational-wave detectors (Bai, Venugopalan, Kuns, Wipf, Markowitz, Wade, Chen & Adhikari 2020) — Proposed using a Mach-Zehnder optomechanical amplifier for phase-sensitive signal amplification in LIGO-class detectors. Performed detailed noise budget analysis showing ~2x strain sensitivity improvement in the 20-100 Hz band for a Voyager-class detector with 15 dB frequency-dependent squeezing, with the primary benefit being tolerance of readout optical losses.

• Quantum radiation pressure noise suppression (Korth, Miao, Corbitt, Cole, Chen & Adhikari 2013) — Proposed a method for increasing the effective quality factor of a mechanical resonator using the optical spring effect and showed how the associated quantum radiation pressure noise can be evaded through sensing and feedback control. This work established the theoretical framework for controlling optomechanical noise that PSOMA relies upon.

• Squeezed light optimization for detector design (Richardson et al. 2022) — Optimized the signal recycling cavity and arm cavity design of LIGO A+ for maximum squeezing performance, accounting for realistic errors. The interplay between signal recycling and squeezing that this work characterized is directly relevant to PSOMA’s compatibility with squeezed vacuum injection.

• LIGO Voyager design (Adhikari et al. 2020) — The cryogenic silicon interferometer design that motivates next-generation quantum noise reduction techniques including PSOMA. Established the baseline detector parameters against which PSOMA’s performance is evaluated.

---

Current status and open questions

Status: PSOMA remains a theoretical proposal. No experimental demonstration has been performed, either at tabletop scale or in a prototype interferometer. The concept was published in 2020 and has attracted interest as a potential addition to third-generation detector designs.

Key open questions:

• Experimental demonstration: Can a phase-sensitive optomechanical amplifier be demonstrated in a tabletop experiment? The Caltech 40-meter prototype interferometer is a natural venue for a first test. Even a modest demonstration — say, 20 dB of phase-sensitive gain at audio frequencies — would validate the concept.

• Stability and control: The amplifier requires precise phase locking of the pump laser to the signal field. In a km-scale interferometer with seismic noise, thermal drifts, and multiple coupled control loops, how robust is this phase lock? What bandwidth is needed for the phase-locking servo?

• Compatibility with the full control system: Advanced LIGO has dozens of coupled control loops managing alignment, length, and frequency of multiple cavities. Adding a Mach-Zehnder amplifier introduces additional degrees of freedom. How do the amplifier control loops interact with the existing interferometer controls?

• Amplifier thermal noise: The noise budget in Bai et al. (2020) shows that amplifier suspension thermal noise and coating Brownian noise contribute significantly at low and mid frequencies, respectively. Can these be reduced by using smaller, lighter test masses with advanced coatings?

• Pump noise coupling: Intensity and frequency noise on the pump laser couple into the amplified output. What pump laser specifications are needed, and are they achievable with current technology?

• Bandwidth engineering: The gain bandwidth is set by the optical spring frequency, which depends on the circulating power and cavity geometry. Can the gain profile be shaped to provide more uniform enhancement across the 10-300 Hz band, rather than the steeply falling $1/\Omega^2$ response?

---

Key references

The PSOMA proposal

• Bai, Venugopalan, Kuns, Wipf, Markowitz, Wade, Chen & Adhikari, “Phase-sensitive optomechanical amplifier for quantum noise reduction in laser interferometers,” Phys. Rev. A 102, 023507 (2020). DOI:10.1103/PhysRevA.102.023507 — The foundational paper proposing PSOMA for GW detectors.

Phase-sensitive amplification theory

• Caves, “Quantum limits on noise in linear amplifiers,” Phys. Rev. D 26, 1817 (1982). DOI:10.1103/PhysRevD.26.1817 — The quantum limit on amplifiers; establishes that phase-sensitive amplifiers can be noiseless.
• Clerk, Devoret, Girvin, Marquardt & Schoelkopf, “Introduction to quantum noise, measurement, and amplification,” Rev. Mod. Phys. 82, 1155 (2010). DOI:10.1103/RevModPhys.82.1155 — Comprehensive review of quantum limits on measurement and amplification.
• Miao, Yang, Martynov & Adhikari, “Quantum correlations of light mediated by gravity,” Phys. Rev. A 101, 063804 (2020). DOI:10.1103/PhysRevA.101.063804 — Quantum optomechanical correlations relevant to amplifier design.

Optomechanical interactions in GW detectors

• Korth, Miao, Corbitt, Cole, Chen & Adhikari, “Suppression of quantum-radiation-pressure noise in an optical spring,” Phys. Rev. A 88, 033805 (2013). DOI:10.1103/PhysRevA.88.033805 — Radiation pressure noise evasion in optical springs.
• Buonanno & Chen, “Signal recycled laser-interferometer gravitational-wave detectors as optical springs,” Phys. Rev. D 65, 042001 (2002). DOI:10.1103/PhysRevD.65.042001 — Signal recycling as optical spring; foundation for PSOMA concept.
• Corbitt, Chen, Khalili, Ottaway, Vyatchanin, Whitcomb & Mavalvala, “Squeezed-state source using radiation-pressure-induced rigidity,” Phys. Rev. A 73, 023801 (2006). DOI:10.1103/PhysRevA.73.023801 — Optomechanical squeezing from radiation pressure.
• Caves & Schumaker, “New formalism for two-photon quantum optics. I. Quadrature phases and squeezed states,” Phys. Rev. A 31, 3068 (1985). DOI:10.1103/PhysRevA.31.3068 — The two-photon formalism for describing quadrature amplitudes and squeezed states; the mathematical language underlying PSOMA’s phase-sensitive amplification.

Frequency-dependent squeezing (deployed in LIGO)

• Ganapathy et al., “Broadband quantum enhancement of the LIGO detectors with frequency-dependent squeezing,” Phys. Rev. X 13, 041021 (2023). DOI:10.1103/PhysRevX.13.041021 — First demonstration of broadband quantum noise reduction in LIGO.
• Richardson, Markowitz, Banks, McCuller, Barsotti, Rollins, Yap, Ward, Adhikari, Arai & Fritschel, “Optimizing gravitational-wave detector design for squeezed light,” Phys. Rev. D 105, 102002 (2022). DOI:10.1103/PhysRevD.105.102002 — Optimizing signal recycling for squeezing performance.

Speed meters and alternative topologies

• Chen, “Sagnac interferometer as a speed-meter-type, quantum-nondemolition gravitational-wave detector,” Phys. Rev. D 67, 122004 (2003). DOI:10.1103/PhysRevD.67.122004 — Speed meter proposal for QND measurement.
• Danilishin et al., “A new quantum speed-meter interferometer: measuring speed to search for intermediate mass black holes,” Light: Science & Applications 7, 11 (2018). DOI:10.1038/s41377-018-0004-2 — Recent speed meter design.

GW detector context

• Adhikari et al., “A cryogenic silicon interferometer for gravitational-wave detection,” CQG 37, 165003 (2020). DOI:10.1088/1361-6382/ab9143 — LIGO Voyager design establishing the detector parameters for PSOMA analysis.
• Ma, Miao, Pang, Evans, Zhao, Adhikari, Fritschel, Chen & Harms, “Proposal for gravitational-wave detection beyond the standard quantum limit through EPR entanglement,” Nature Phys. 13, 776 (2017). DOI:10.1038/nphys4118 — EPR entanglement approach to surpassing the SQL; an alternative to PSOMA that also exploits quantum correlations in the interferometer output.

---

Further reading

For readers who want to go deeper:

• Aspelmeyer, Kippenberg & Marquardt, “Cavity optomechanics,” Rev. Mod. Phys. 86, 1391 (2014). DOI:10.1103/RevModPhys.86.1391 — The definitive review of optomechanical systems, covering optical springs, parametric amplification, and quantum limits.
• Danilishin & Khalili, “Quantum measurement theory in gravitational-wave detectors,” Living Rev. Relativ. 15, 5 (2012). DOI:10.12942/lrr-2012-5 — Comprehensive treatment of quantum noise in GW detectors, including the SQL and strategies for beating it.
• Kimble, Levin, Matsko, Thorne & Vyatchanin, “Conversion of conventional gravitational-wave interferometers into quantum nondemolition interferometers by modifying their input and/or output optics,” Phys. Rev. D 65, 022002 (2001). DOI:10.1103/PhysRevD.65.022002 — The foundational paper on using squeezed light and variational readout to beat the SQL in LIGO-type detectors.